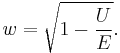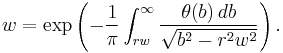Oleg Firsov
Oleg Borisovich Firsov (Russian: Олег Борисович Фирсов, June 13 [OS May 31] 1915, Petrograd – April 2, 1998, Moscow) – was a Russian Soviet physicist-theorist known for his work on atomic interaction. He was awarded the Lenin Prize in 1972 for a series of work titled "Elementary processes and non-elastic scattering at nuclear collisions".
Contents |
Biography
Firsov was the son of Boris Nilovich Firsov (1888–1920), one of the first Russian pilots, and Olga Vladimirovna von Walden (by mother Golitsyn, 1892–1920). He lost his parents at the age of 4, and grew up in an orphanage.
He graduated with an undergraduate degree in physics from Leningrad State University in 1938, and remained there until the end of World War II. Staying in the city, he then moved to the Ioffe Physico-Technical Institute in Leningrad, where he obtained his PhD in 1947 under Yakov Frenkel's supervision. In 1955, he was invited by Igor Kurchatov to Moscow. He joined the Kurchatov Institute of Atomic Energy where worked until 1994, when he became severely ill.
He was married to the physicist Victoria Yevgenyevna Lichko (1915–2004). Their daughter is the composer Elena Firsova (b. 1950).
Work
Firsov's PhD thesis and first publications were devoted to gas discharges and yielded a model of spark formation and propagation, which is still used to describe both natural lightning and laboratory discharges. He returned to this topic in the 1970s to develop a more accurate theory.
Firsov is known among physicists for his studies of the quasi-molecular approach in the quantum mechanical theory of atomic collisions. In a 1951 paper, he presented an elegant analytical solution to the complicated problem of resonant charge exchange during hydrogen-hydrogen collisions. Since then, the quasi-molecular approach has been used in many other fields related to the physics of atomic collisions.
In 1953, Firsov devised the solution to the so-called inverse collision problem in which a scattering potential is inferred from known values of the scattering cross-section.
At the beginning of the 1950s, when work on controlled fusion reactions had just started at Kurchatov, solving the problem of charge exchange for the confinement of a plasma in a magnetic system was crucial. Accordingly, Firsov was invited to tackle the problem. Applying his gift for discerning the root of a problem, he considered plasma permeation through a picket fence magnetic system and, in 1957, was the first to theoretically determine the width of a magnetic gap for a cusp system. His approach is still used.
Around the same time, Firsov also carried out two of his best-known works. In 1957, he found the exact upper and lower limits of the interaction potential between two atoms in the Thomas-Fermi approximation. Since these limits turned out to be close to each other, the potential could be determined accurately. Firsov suggested a simple approximation of this potential that is convenient to use and is now referred to as the Firsov potential. In 1959, he proposed a formula for inelastic energy losses in an atomic collision on the basis of a very clear physical picture in which a number of electrons are exchanged between the colliding atoms. This formula has not only found a wide range of application in the physics of ion beams and radiation effects, but has also stimulated considerable theoretical activity.
In 1966 and 1970, Firsov published two papers on the reflection of particles from a solid surface.
During the last few years of his life, Firsov investigated one of the most fundamental cosmological problems-identifying the nature of dark matter. He proposed that the invisible mass in the universe is dust of ordinary matter.
Among his pupils were physicists Mikhail Chibisov, Yuri Martynenko, Boris Smirnov and Edward Lozansky. He had particularly close scientific links with the experimentalist Vera Yurasova, with whom he also worked in the Russian Academy of Sciences Council for Plasma Physics.
Inverse collision problem
Let us consider the scattering of particles with energy  in a repulsive field
in a repulsive field 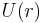 and introduce the quantity
and introduce the quantity
Firsov proved that this quantity is implicitly related to the angle of scattering 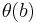 (
( is the impact parameter) by the formula
is the impact parameter) by the formula
Bibliography
- Lozansky, E.D. and Firsov O.B.: THE Theory of the Initial Stage of Streamer Propagation
- Firsov O.B.: in Fizika Plazmy i Problema Upravlyaemykh Termoyadernykh Reaktsiî Vol. 3 (Plasma Physics and Thermonuclear Research) (Ed. M A Leontovich) (Moscow: Izd. AN SSSR, 1958) p. 327
- Lozansky, E.D. and Firsov O.B.: The Theory of the Spark, 1975 (Лозанский Э.Д., Фирсов О.Б. Теория искры. 1975. 272 с.)